Gravitational Potential Energy

Three masses $m, 2 \mathrm{m}$ and $3 \mathrm{m}$ are arranged in two triangular configurations as shown in figure $1$ and figure $2$ . Work done by an external agent in changing the configuration from figure $1$ to figure $2$ is

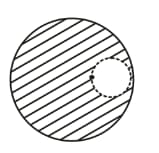
A spherical portion of radius $\frac{R}{2}$ is removed from a solid sphere of mass $M$ and radius $R$ as shown in the figure. Taking gravitational potential $V=0$ at $r=\infty$, the potential at the centre of the cavity thus formed is $(G=\text{gravitational constant})$,

What is the minimum energy required to launch a satellite of mass $\mathrm{m}$ from the surface of a planet of mass $\mathrm{M}$ and radius $\mathrm{R}$ in a circular orbit at an altitude of $2\mathrm{R}?$

A particle of mass $50 \mathrm{g}$ is kept on the surface of a uniform sphere of mass $120 \mathrm{k}\mathrm{g}$ and radius $50 \mathrm{c}\mathrm{m}$. Find the work to be done against the gravitational force between them (in $\mathrm{n}\mathrm{J}$) to take the particle far away from the sphere. (Take $G=6.67\times {10}^{-11} \mathrm{N} {\mathrm{m}}^2 \mathrm{k}{\mathrm{g}}^{-2}$).

A small $2 \mathrm{k}\mathrm{g}$ mass moved slowly from the surface of earth to a height of $6.4\times {10}^6 \mathrm{m}$ above the earth. Find the work done [in mega joule].(Radius of earth is $6.4\times {10}^6$ $\mathrm{m}$)

Consider a planet moving in an elliptical orbit around the Sun. The work done on the planet by the gravitational force of the Sun:

Which of the following are correct?

A person brings a mass of $1 \mathrm{k}\mathrm{g}$ from infinity to a point $A$. Initially the mass was at rest but it moves with a speed of $2 \mathrm{m}/\mathrm{s}$ as it reaches $A$. The work done by the person on the mass is $-3 \mathrm{J}$. The potential at $A$ is:

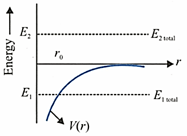
If both the objects have the same $PE$ curve as shown in the figure, then:

In the graph shown, the potential energy of the earth-satellite system is shown by a solid line as a function of distance $r$ (the separation between the earth's centre and satellite). The total energy of the two objects which may or may not be bounded to the earth is shown in the figure by dotted lines. If the object having total energy $E_1$ is having the same $P.E.$ curve as shown in the figure, then
  

As Pluto moves from the perihelion to the aphelion, the work done by gravitational pull of Sun on Pluto is:

At perihelion, the gravitational potential energy of Pluto in its orbit has:

From a solid sphere of mass $M$ and radius $R$, a spherical portion of radius $\frac{\mathrm{R}}{2}$ is removed, as shown in the figure. Taking gravitational potential $\mathrm{V}=0$ at $\mathrm{r}=\infty$ the potential at the centre of the cavity thus formed is $(\mathrm{G}=\text{Universal gravitational constant})$.

The gravitational field intensity at a point $\mathrm{10,000} \mathrm{km}$ from the centre of the earth is $4.8$ $\mathrm{N}\mathrm{ }\mathrm{k}{\mathrm{g}}^{-1}$. The gravitational potential at that point is,

A non - homogeneous sphere of radius $R$ has the following density variation:
$\rho =\left\{\begin{array}{c}{\rho }_{\mathit{0}} ; 0<r\le R/3\\ {\rho }_{\mathit{0}}/2 ; (R/3)<r\le (\mathit{3}R/4)\\ {\rho }_{\mathit{0}}/8 ; (\mathit{3}R/4)<r\le R \end{array}\right.$
Where ${\rho }_0$ is constant. The gravitational field at a distance $2R$ from from the centre of the sphere is:

An asteroid of mass $m$ is approaching earth, initially at a distance $10R_{\mathrm{E}}$ with speed $v_{\mathrm{i}}$. It hits the earth with a speed $v_{\mathrm{f}}$ ($R_{\mathrm{E}}$ and $M_{\mathrm{E}}$ are radius and mass of earth), then

A rocket is fired vertically from the surface of the earth with a speed $\mathrm{v}$. How far from the earth does the rocket go before returning to the earth?
(Where ${\mathrm{R}}_{\mathrm{E}}$ is the radius or the earth and $\mathrm{g}$ is acceleration due to gravity)

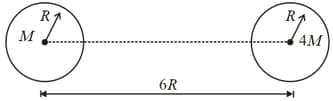
Two uniform solid spheres of equal radii $R$, but with masses $M$ and $4M$; have a centre to centre separation $6R$, as shown in figure. A particle of mass $m$ is projected from the surface of the sphere of mass $M$ directly towards the centre of the second sphere. The minimum speed of the projectile so that it reaches the surface of the second sphere is 

The change in potential energy when a body of mass $m$ is taken to a height $n{R}_{\mathit{E}}$ above the Earth's surface is:
($R_E$ = radius of the earth)

A rope of length $l$, mass $M$ is kept on smooth surface such that ${\left(\frac{1}{n}\right)}^{th}$ part of it is hanging from the surface. Find work done to lift the rope on surface.